Department of Chemistry

Welcome to the Department of Chemistry at Durham
Durham’s Chemistry Department delivers research-led and socially relevant chemical education, with alumni that are innovators and leaders in chemical industries and beyond. Our research is transformational and translational, with specific strengths in: developing underpinning spectroscopic and computational methods; devising novel processes and materials for sustainable chemistry; and creating molecules, formulations, technologies and global networks to improve health. Our values foster a supportive, diverse community in a small historic city with deep regional roots and a global reach.
Study with us
Undergraduate Study
We offer both BSc and MChem undergraduate courses, many accredited by the Royal Society of Chemistry.
Postgraduate Study
Discover our MSc and PhD research degrees at a world-leading university.
What's new?
Twenty Durham researchers appointed to REF 2029 sub-panels
Twenty of our researchers will take important roles in assessing UK universities’ research quality.

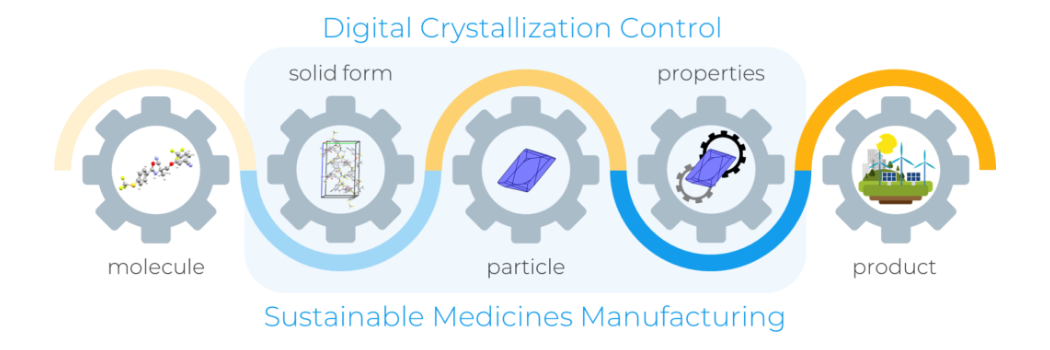
Pioneering research to support digital innovation in pharmaceuticals
Women in chemistry: Q&A with Professor Aurora J. Cruz-Cabeza
Breakthrough drug for motor neurone disease shows promise in new study
Professor Paul Denny and team win prestigious MRC Outstanding Team Impact Prize
Prof. A. Beeby granted access to the Utrecht Psalter for special research
The global team on Neglected Tropical Diseases Wins the Durham Global SDG Award 2023
Twenty Durham researchers appointed to REF 2029 sub-panels
Twenty of our researchers will take important roles in assessing UK universities’ research quality.

Pioneering research to support digital innovation in pharmaceuticals
Breakthrough drug for motor neurone disease shows promise in new study
Our research
We are a vibrant, research-led department with an international reputation for cutting-edge science.
Diversity and Inclusion
Meet us and get involved
Our facilities and equipment
We provide services to our in-house researchers and students. We also work with many UK and overseas companies and other universities and research institutions.
Get in touch
Enquiries about Chemistry and our courses should be sent via the emails below:
Department of Chemistry
Durham University
Stockton Road
Durham
DH1 3LE
United Kingdom
Telephone (UK): +44 (0191) 334 2076
Telephone (International): +44 191 334 2000
Questions about studying here?
Check out our list of FAQs or submit an enquiry form.
Your Durham prospectus
Order your personalised prospectus and College guide here.



/prod01/prodbucket01/media/durham-university/departments-/chemistry/study/ug-study/56633.jpg)
/prod01/prodbucket01/media/durham-university/departments-/chemistry/study/ug-study/56632.jpg)


.png)




/prod01/prodbucket01/media/durham-university/departments-/computer-science/83496.jpg)
/prod01/prodbucket01/media/durham-university/departments-/chemistry/about/staff/Our-People.jpeg)
/prod01/prodbucket01/media/durham-university/departments-/computer-science/81551.jpg)
/prod01/prodbucket01/media/durham-university/departments-/computer-science/Athena-Swan-Bronze.jpg)
